Ever wondered why mean, median, and mode are always mentioned together in math class? It’s not just some random grouping—there’s a deeper connection between these three statistical measures that can unlock a whole new understanding of data analysis. Whether you’re a student trying to ace your exams or a professional diving into data science, mastering mean median mode connections is crucial. Let’s break it down together and make stats less intimidating and more relatable.
Now, before we dive headfirst into the world of numbers, let me tell you something cool. Statistics isn’t just about crunching numbers—it’s about telling stories. And mean, median, and mode? They’re the main characters in this story. Each one plays a unique role in helping us make sense of the data we encounter every day. So, buckle up because we’re about to explore their relationships and how they work together.
One thing I want you to keep in mind is that these three measures aren’t just standalone concepts. They’re interconnected in ways that can reveal hidden patterns and insights in your data. By the end of this article, you’ll have a solid understanding of how mean median mode connections can help you interpret data more effectively. Let’s get started!
Read also:Veronica Duterte Daughter Mira The Untold Story You Wont Believe
What Are Mean, Median, and Mode?
Alright, let’s start with the basics. Before we jump into the connections, it’s important to understand what each of these terms means individually. Think of them as your statistical besties—each has its own quirks and strengths.
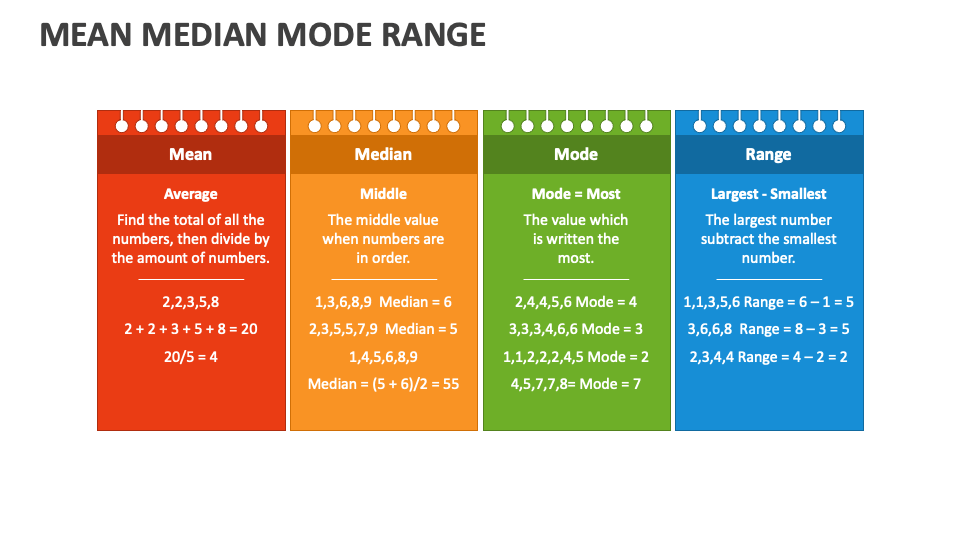
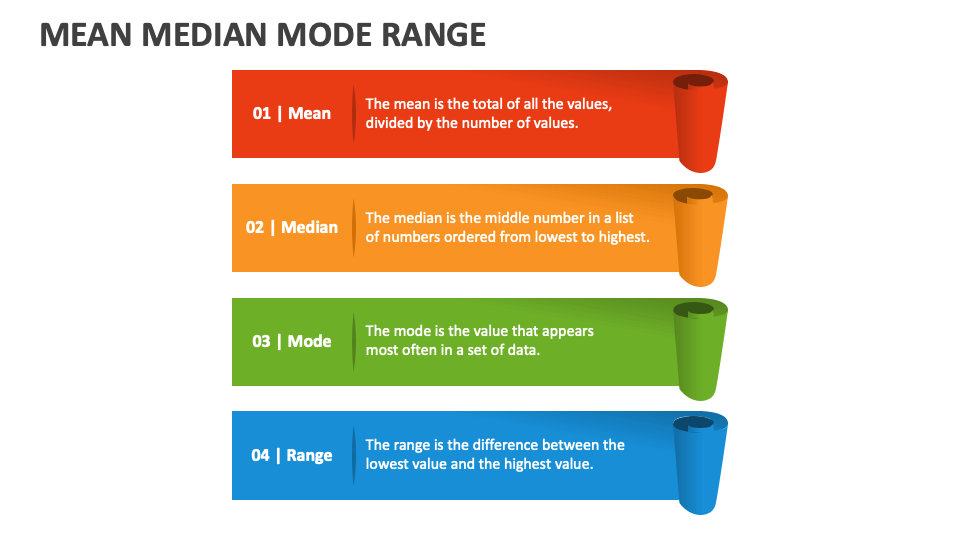
The mean is like the popular kid in school. It’s the average of all the numbers in a dataset. You add up all the values and divide by how many there are. Simple, right? But here’s the thing—mean can be influenced by outliers, those pesky numbers that are way higher or lower than the rest.
Then we’ve got the median, the chill one in the group. It’s the middle value when you arrange all the numbers in order. If there’s an even number of values, you take the average of the two middle ones. Median doesn’t care about outliers—it’s more focused on the center of the data.
And last but not least, we have the mode, the unique one in the bunch. It’s the number that appears most frequently in the dataset. Some datasets might have no mode, while others can have multiple modes. Mode is all about identifying patterns in your data.
Why Are Mean Median Mode Connections Important?
Here’s the deal—mean, median, and mode aren’t just random stats terms. They’re tools that help us understand data better. When you analyze a dataset, looking at all three gives you a more complete picture. It’s like using different lenses to examine the same object.
For example, if you’re analyzing household incomes in a neighborhood, the mean might give you an idea of the average income. But if there are a few super-rich households, the mean could be skewed. That’s where the median comes in—it gives you a more accurate sense of what the typical income is. And if certain income levels appear more frequently, the mode can highlight those trends.
Read also:Janet Lee Constantine The Remarkable Story Of A Trailblazing Leader
In short, understanding mean median mode connections helps you avoid being misled by data. It’s about seeing the full story, not just one side of it. And trust me, in today’s data-driven world, that’s a skill you’ll want to have.
Biases and Limitations of Each Measure
Now, let’s talk about the not-so-perfect sides of our statistical trio. Each measure has its own biases and limitations, and recognizing them is key to using them effectively.
Limitations of the Mean
- The mean is highly sensitive to outliers. A single extreme value can drastically change the result.
- It doesn’t always represent the typical value in a dataset, especially if the data is skewed.
Limitations of the Median
- While the median is robust against outliers, it doesn’t take into account the actual values of the data points.
- It’s less precise than the mean when working with large datasets.
Limitations of the Mode
- Some datasets might have no mode, making it less useful in certain situations.
- In cases with multiple modes, it can be hard to interpret which one is truly significant.
Understanding these limitations helps you choose the right measure for your specific situation. Sometimes, using a combination of all three gives you the best results.
Practical Applications of Mean Median Mode Connections
Okay, enough theory. Let’s see how mean median mode connections play out in real life. Whether you’re in business, healthcare, education, or any other field, these concepts are everywhere.
Business Analytics
In the business world, mean median mode connections help companies make data-driven decisions. For instance, a retailer might use the mean to calculate average sales, the median to identify the typical customer spending, and the mode to spot the most popular product category.
Healthcare
In healthcare, these measures are used to analyze patient data. The mean might show the average recovery time, the median can highlight the typical case, and the mode can reveal the most common symptoms or conditions.
Education
Teachers use mean median mode connections to evaluate student performance. The mean gives an overview of class performance, the median shows the middle student’s score, and the mode highlights the most frequent grade.
See how versatile these concepts are? They’re not just for math class—they’re tools for solving real-world problems.
How to Calculate Mean Median Mode Connections
Let’s get down to the nitty-gritty. Calculating mean, median, and mode isn’t rocket science, but it’s important to do it right. Here’s a quick guide:
Calculating the Mean
Take all the numbers in your dataset, add them up, and divide by how many numbers there are. Simple as that.
Calculating the Median
Arrange your numbers in order from smallest to largest. If there’s an odd number of values, the median is the middle one. If it’s even, take the average of the two middle numbers.
Calculating the Mode
Look for the number that appears most frequently. If no number repeats, there’s no mode. If multiple numbers have the same frequency, you have multiple modes.
These calculations might seem basic, but they’re the foundation of data analysis. Practice them enough, and they’ll become second nature.
Exploring Skewed Distributions
Now, here’s where things get interesting. Not all datasets are perfectly symmetrical. Some are skewed, meaning the data isn’t evenly distributed. In these cases, mean median mode connections become even more important.
Positive Skew
In a positively skewed distribution, the tail points to the right. The mean is usually higher than the median, and the mode is the lowest value.
Negative Skew
In a negatively skewed distribution, the tail points to the left. The mean is usually lower than the median, and the mode is the highest value.
Understanding skewness helps you interpret the relationships between mean, median, and mode more accurately. It’s like reading between the lines of your data.
Advanced Statistical Techniques
Once you’ve mastered the basics, you can move on to more advanced techniques. Concepts like standard deviation, variance, and percentiles build on the foundation of mean median mode connections.
Standard Deviation
This measures how spread out your data is. A low standard deviation means the values are close to the mean, while a high one indicates more variability.
Variance
Variance is similar to standard deviation but is expressed as the square of the deviation. It’s another way to quantify data spread.
Percentiles
Percentiles divide your data into 100 equal parts. They help you understand where a particular value stands in relation to the rest of the dataset.
These techniques add depth to your analysis and allow you to explore your data in greater detail.
Real-World Case Studies
Let’s look at some real-world examples to see mean median mode connections in action.
Case Study 1: Income Analysis
A city planner is analyzing household incomes. The mean income is $70,000, but the median is only $50,000. This suggests the presence of high-income outliers skewing the mean. The mode, $45,000, indicates the most common income level.
Case Study 2: Test Scores
A teacher is evaluating student test scores. The mean score is 75%, the median is 78%, and the mode is 80%. This shows a relatively balanced distribution with a slight positive skew.
These case studies highlight how mean median mode connections can reveal insights that might be missed with a single measure.
Tools and Resources for Data Analysis
In today’s digital age, you don’t have to do all the calculations by hand. There are plenty of tools and resources to help you analyze data more efficiently.
Excel
Microsoft Excel is a powerful tool for calculating mean, median, and mode. It also offers advanced functions for data visualization and analysis.
R and Python
If you’re into programming, R and Python are excellent choices for statistical analysis. They offer a wide range of libraries and packages to simplify complex calculations.
Online Calculators
For quick and easy calculations, online calculators are a great option. They’re user-friendly and accessible from anywhere.
Using the right tools can save you time and effort, allowing you to focus on interpreting the results.
Future Trends in Data Analysis
As technology continues to evolve, so does the field of data analysis. New tools and techniques are emerging that make it easier to explore mean median mode connections and beyond.
Artificial Intelligence
AI is revolutionizing data analysis by automating complex processes and providing deeper insights. It can identify patterns and correlations that might be missed by human analysts.
Big Data
With the rise of big data, the importance of mean median mode connections is growing. These measures help make sense of massive datasets and extract meaningful information.
Staying up-to-date with these trends will keep you ahead of the curve in the world of data analysis.
Conclusion: Mastering Mean Median Mode Connections
So, there you have it—a comprehensive look at mean median mode connections. These three measures might seem simple on the surface, but they’re powerful tools for understanding data. By recognizing their strengths and limitations, and using them together, you can unlock insights that lead to better decision-making.
Remember, data analysis isn’t just about numbers—it’s about telling stories. And mean, median, and mode are the key characters in that story. So, whether you’re a student, a professional, or just someone curious about stats, mastering these concepts will serve you well.
Now, it’s your turn. Take what you’ve learned and apply it to your own data. And don’t forget to share this article with your friends and colleagues. The more people understand mean median mode connections, the better equipped we all are to navigate the data-driven world we live in.
Table of Contents
- What Are Mean, Median, and Mode?
- Why Are Mean Median Mode Connections Important?
- Biases and Limitations of Each Measure
- Practical Applications of Mean Median Mode Connections
- How to Calculate Mean Median Mode Connections
- Exploring Skewed Distributions
- Advanced Statistical Techniques
- Real-World Case Studies
- Tools and Resources for Data Analysis
- Future Trends in Data Analysis